Python算法之动态规划(Dynamic Programming)解析:二维矩阵中的醉汉(魔改版leetcode出界的路径数)

    现在很多互联网企业学聪明了，知道应聘者有目的性的刷Leetcode原题，用来应付算法题面试，所以开始对这些题进行“魔改”，比如北京某电商平台的这道题：

    有一个正方形的岛，使用二维方形矩阵表示，岛上有一个醉汉，每一步可以往上下左右四个方向之一移动一格，如果超出矩阵范围他就死了，假设每一步的方向都是随机的(因为他是醉的)，请计算n步以后他还活着的概率。

例如：输入矩阵大小2*2，起点(0,0)，随机走出一步 n = 1

输出0.5  也就是有一半的几率还活着

例如：输入矩阵大小3*3，起点(1,1)，随机走出一步 n = 1

输出1  也就是百分之百还活着

    乍一看有点懵，但是提取关键字：二维矩阵、上下左右四个方向、矩阵范围、n步，有没有感到很熟悉？刷过Leetcode的同学一定已经联想到了Leetcode原题第576题：出界的路径数，难度等级为中等。

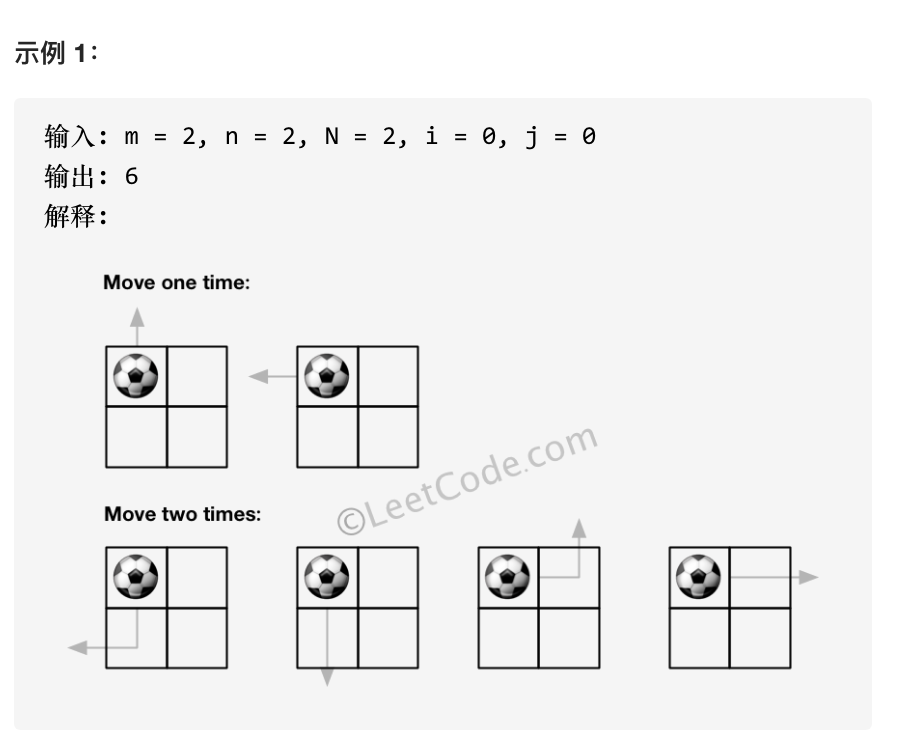
给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。

    和魔改版的题联系起来，所谓醉汉“死了”，其实就是移出边界，而每走一步都会有四种可能，所以所谓的“存活率”也就是当我们算出移出边界的路径数量之后，再除以方向的基数4，就可以算出“存活率”，相反也可以推算“死亡率”，归根结底，魔改版题的题眼还是算出移出边界的路径数，并不是最后问的“存活率”问题，这题只是用了一个并不是很讲究的障眼法，很有可能是该电商平台老板让手下的某个研发出道算法题招人用，而该研发已经被需求搞的晕头转向，无奈之下随便从leetcode复制了一道出来，随便改了改。

    至于解法，下意识想到并且非常好理解的解法就是利用BFS(Breadth First Search 广度优先)，因为醉汉最多只能移动N次，我们只要bfs依次遍历如果发现出界，就代表死亡，进行累加1，当bfs的深度大于N的时候break结束。理论上是没有任何问题。

import collections
def how_likely_alive(m,n,N,i,j):
    mod = 10**9 + 7
    Q = collections.deque([(i,j,0)])
    res = 0
    while Q:
        x,y,step = Q.popleft()
        if step > N: break
        if 0<=x<m and 0<=y<n:
            Q.append((x+1,y,step+1))
            Q.append((x-1,y,step+1))
            Q.append((x,y+1,step+1))
            Q.append((x,y-1,step+1))
        else:
            res += 1
    num = res % mod
    if num == 0:
        return 1
    else:
        return num / 4


print(how_likely_alive(2,2,1,0,0))

    一般情况下，如果该岗位的技术要求并不高，使用bfs基本就算过关了，但是如果面试官想来一次压力面试（所谓压力面试就是想探探你的底），看看你的极限在哪里，就会要求你用效率更高的算法来解题。（这里需要简单分辨一下压力面试还是故意刁难，压力面试如果不会的话，礼貌询问就能拿到答案，而如果连面试官都不知道面试的答案，那肯定就是故意刁难了，也就没有面下去的必要了）。

    我们再回到题目中想一想，魔改版题目并没有定义醉后随机走的步数N的范围，假设N的取值范围达到了50，我们对任意一个坐标点bfs有四个方向进行遍历，同时考虑往回走的可能性，那么复杂度达到了N的四倍，这个效率显然不会令人满意，所以当N相对小的情况下,比如只走1步，bfs是最优解，而范围过大就需要考虑dp了。

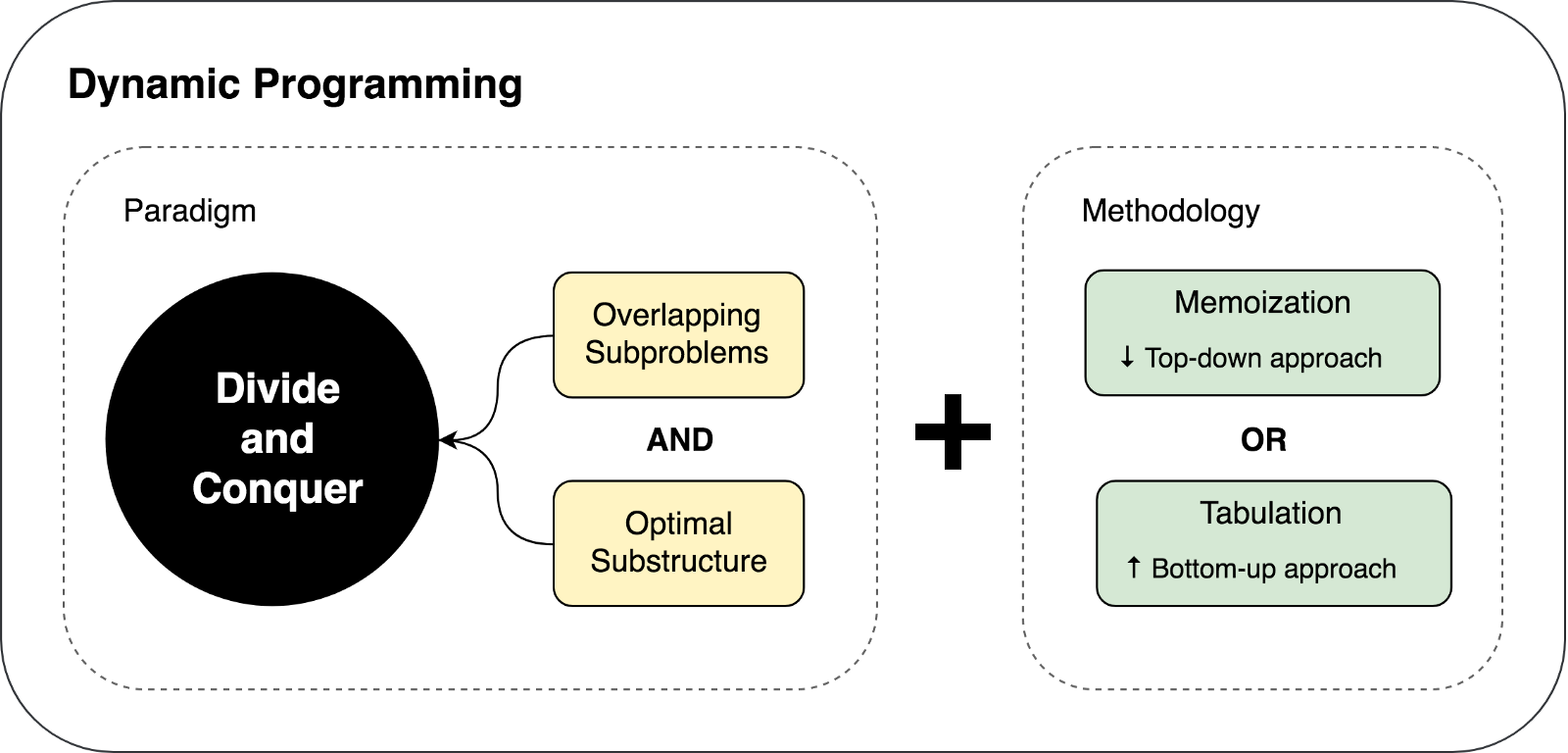
    dp(Dynamic Programming)算法即是业界大名鼎鼎的动态规划算法了，其核心思路是把一个复杂的大问题拆成若干个子问题，通过解决子问题来逐步解决大问题，是不是和分治法有点像？关于分治算法可以参考这篇文章：当我们谈论算法我们在谈论什么:由疫情核酸检测想到的分治算法(Divide-and-Conquer),但是和分治法有区别的地方是，使用动态规划思想有个前提：当且仅当每个子问题都是离散的（即每个子问题都不依赖于其他子问题时），才能使用动态规划。

    再次回到题目，假设这个醉汉在第 N 步到达 (mi, nj) 位置有 dp[N][mi][nj] 种路径，可以假设一下当前状态如何从上一步移动中得来。其实就是上下左右四个方向移动过来的，而移动步数则是 N-1。

def how_likely_alive(m, n, N, i, j):

    tmp=[[[0 for i in range(n)] for j in range(m)] for k in range(N+1)]
    for k in range(1,N+1):
        for p in range(m):
            for q in range(n):
                if 0==p:
                    up=1
                else:
                    up=tmp[k-1][p-1][q]
                if m-1==p:
                    down=1
                else:
                    down=tmp[k-1][p+1][q]
                if 0==q:
                    left=1
                else:
                    left=tmp[k-1][p][q-1]
                if n-1==q:
                    right=1
                else:
                    right=tmp[k-1][p][q+1]
                tmp[k][p][q]=(up+down+left+right)%1000000007

    num = tmp[N][i][j]
    if num == 0:
        return 1
    else:
        return num / 4
    return num
print(how_likely_alive(2,2,1,0,0))

    结语：Leetcode算法题浩如烟海，想要每一道题都了如指掌，个人感觉难度不小，但是从这道二维矩阵中的醉汉来看，企业就算想要“魔改”，也是万变不离其宗，多多少少都有迹可循，所以我们在刷题的过程中，应该本着宁缺毋滥的原则，真实的掌握算法核心思想，才能够做到举一反三、百战不殆。