动手造轮子自己实现人工智能神经网络(ANN)，解决鸢尾花分类问题Golang1.18实现

    人工智能神经网络（ Artificial Neural Network，又称为ANN）是一种由人工神经元组成的网络结构，神经网络结构是所有机器学习的基本结构，换句话说，无论是深度学习还是强化学习都是基于神经网络结构进行构建。关于人工神经元，请参见：人工智能机器学习底层原理剖析,人造神经元,您一定能看懂,通俗解释把AI“黑话”转化为“白话文”。

    机器学习可以解决什么问题

    机器学习可以帮助我们解决两大类问题：回归问题和分类问题，它们的主要区别在于输出变量的类型和预测目标的不同。

    在回归问题中，输出变量是连续值，预测目标是预测一个数值。例如，预测房价、预测销售额等都是回归问题。通常使用回归模型，如线性回归、决策树回归、神经网络回归等来解决这类问题。回归问题的评估指标通常是均方误差（Mean Squared Error，MSE）、平均绝对误差（Mean Absolute Error，MAE）等。

    在分类问题中，输出变量是离散值，预测目标是将样本划分到不同的类别中。例如，预测邮件是否是垃圾邮件、预测图像中的物体类别等都是分类问题。通常使用分类模型，如逻辑回归、决策树分类、支持向量机、神经网络分类等来解决这类问题。分类问题的评估指标通常是准确率、精度（Precision）、召回率（Recall）等。

    事实上，机器学习只能解决“可以”被解决的问题，也就是说，机器学习能帮我们做的是提高解决问题的效率，而不是解决我们本来解决不了的问题，说白了，机器学习只能解决人目前能解决的问题，比如说人现在不能做什么？人不能永生，不能白日飞升，也不能治愈绝症，所以你指望机器学习解决此类问题，就是痴心妄想。

     同时，机器学习输入的特征参数和输出的预期结果必须有逻辑相关性，什么意思？比如说我们想预测房价，结果特征参数输入了很多没有任何逻辑相关性的数据，比如历年水稻的出产率，这就是没有逻辑相关性的数据，这样的问题再怎么调参也是无法通过机器学习来解决的。

    此外，回归问题中有一个领域非常引人关注，那就是预测股票价格，国内经常有人说自己训练的模型可以预测某支A股的价格走势，甚至可以精准到具体价格单位。说实话，挺滑稽的，关键是还真有人相信靠机器学习能在A股市场大杀特杀。

    因为，稍微有点投资经验的人都知道，股票的历史数据和未来某个时间点或者某个时间段的实际价格，并不存在因果关系，尤其像A股市场这种可被操控的黑盒环境，连具体特征都是隐藏的，或者说特征是什么都是未知的，你以为的特征只是你以为的，并不是市场或者政策以为的，所以你输入之前十年或者二十年的历史股票数据，你让它预测，就是在搞笑，机器学习没法帮你解决此类问题。

    为什么现在GPT模型现在这么火？是因为它在NLP（自然语言分析）领域有了质的突破，可以通过大数据模型联系上下文关系生成可信度高的回答，而这个上下文关系，就是我们所谓的参数和预期结果的因果关系。

    鸢尾花分类问题

    鸢尾花分类问题是一个经典的机器学习问题，也是神经网络入门的常用案例之一。它的目标是通过鸢尾花的花萼长度、花萼宽度、花瓣长度和花瓣宽度这四个特征来预测鸢尾花的品种，分为三种：山鸢尾（Iris Setosa）、变色鸢尾（Iris Versicolour）和维吉尼亚鸢尾（Iris Virginica）。

    通俗来讲，就是我们要训练一个神经网络模型，它能够根据鸢尾花的四个特征，自动地对鸢尾花的品种进行分类。

    在这个案例中，我们使用了一个包含一个隐藏层的神经网络，它的输入层有4个神经元，代表鸢尾花的4个特征；隐藏层有3个神经元；输出层有3个神经元，分别代表3种鸢尾花的品种：

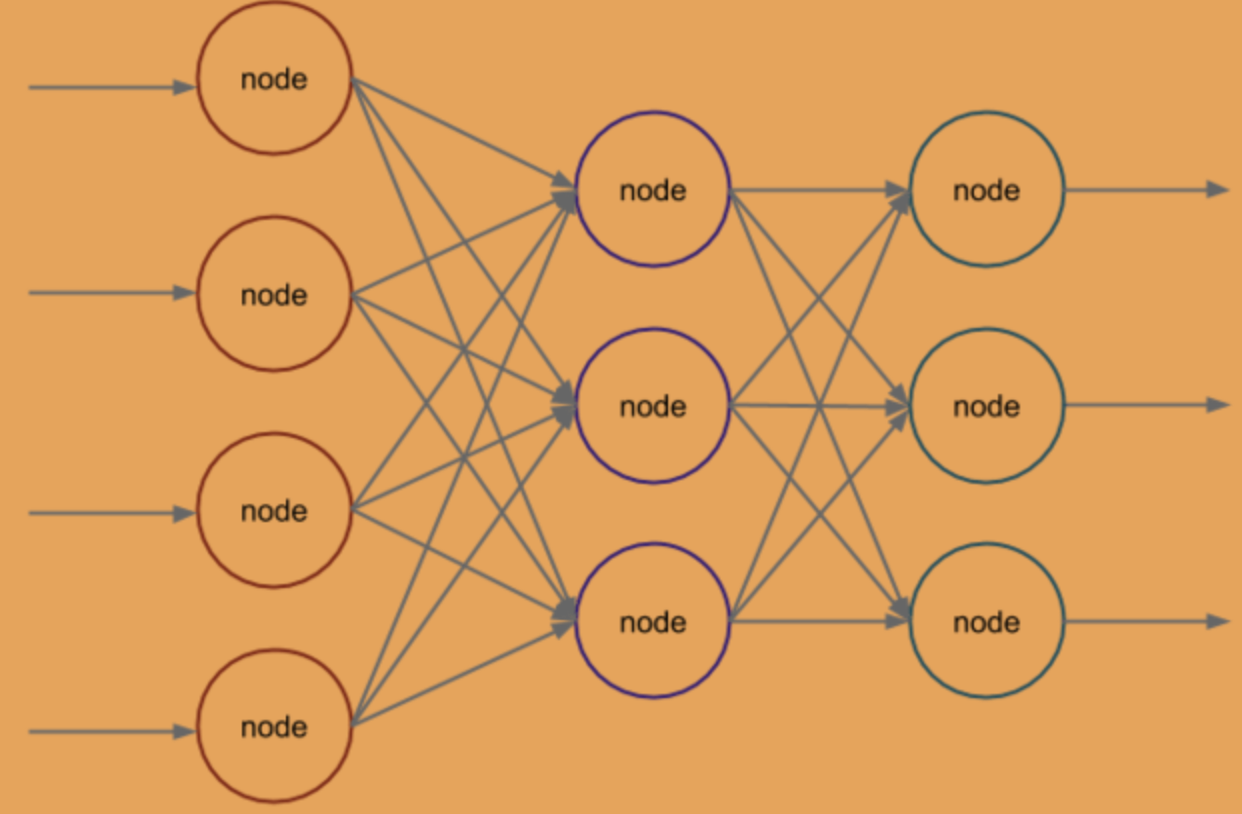
    由此可见，神经网络通常由三层组成：输入层、隐藏层和输出层。

    输入层：输入层接收外部输入信号，是神经网络的起点。它的神经元数量与输入特征的数量相同，每个神经元代表一个输入特征。输入层的主要作用是将外部输入转换为神经网络内部的信号。

    隐藏层：隐藏层位于输入层和输出层之间，是神经网络的核心部分。它的神经元数量可以根据问题的复杂度自由设定，每个神经元接收上一层神经元输出的信号，并进行加权处理和激活函数处理，再将结果传递给下一层神经元。隐藏层的主要作用是对输入信号进行复杂的非线性转换，提取出输入信号中的特征，从而使得神经网络能够对复杂的问题进行处理。

    输出层：输出层是神经网络的终点，它的神经元数量通常与问题的输出数量相同。每个神经元代表一个输出结果，输出层的主要作用是将隐藏层处理后的信号进行进一步处理，并将最终的结果输出。

    在神经网络中，输入信号从输入层开始，通过隐藏层的处理，最终到达输出层。每一层的神经元都与下一层的神经元相连，它们之间的连接可以看成是一种权重关系，权重值代表了两个神经元之间的相关性强度。当神经网络接收到输入信号后，每个神经元都会对这些信号进行加权处理，并通过激活函数将结果输出给下一层神经元，最终形成输出结果。通过不断调整权重和激活函数，神经网络可以学习到输入和输出之间的复杂非线性关系，从而对未知数据进行预测和分类等任务。

    定义神经网络结构体

    在开始训练之前，我们先定义一些需要的结构体和函数：

// neuralNet contains all of the information
// that defines a trained neural network.
type neuralNet struct {
	config  neuralNetConfig
	wHidden *mat.Dense
	bHidden *mat.Dense
	wOut    *mat.Dense
	bOut    *mat.Dense
}

// neuralNetConfig defines our neural network
// architecture and learning parameters.
type neuralNetConfig struct {
	inputNeurons  int
	outputNeurons int
	hiddenNeurons int
	numEpochs     int
	learningRate  float64
}

    这里neuralNet是神经网络结构体，同时定义输入、隐藏和输出层神经元的配置。

    随后声明函数初始化神经网络：

func newNetwork(config neuralNetConfig) *neuralNet {
        return &neuralNet{config: config}
}

    这里返回神经网络的指针。

    除此之外，我们还需要定义激活函数及其导数，这是在反向传播过程中需要使用的。激活函数有很多选择，但在这里我们将使用sigmoid函数。这个函数有很多优点，包括概率解释和方便的导数表达式：

// sigmoid implements the sigmoid function
// for use in activation functions.
func sigmoid(x float64) float64 {
        return 1.0 / (1.0 + math.Exp(-x))
}

// sigmoidPrime implements the derivative
// of the sigmoid function for backpropagation.
func sigmoidPrime(x float64) float64 {
    return sigmoid(x) * (1.0 - sigmoid(x))
}

    实现反向传播

    反向传播是指在前向传播之后，计算神经网络误差并将误差反向传播到各层神经元中进行参数（包括权重和偏置）的更新。在反向传播过程中，首先需要计算网络的误差，然后通过链式法则将误差反向传播到各层神经元，以更新每个神经元的权重和偏置。这个过程也被称为“反向梯度下降”，因为它是通过梯度下降算法来更新神经网络参数的。

    说白了，反向传播就是逆运算，用结果反推过程，这里我们可以编写一个实现反向传播方法的方法，用于训练或优化我们网络的权重和偏置。反向传播方法包括以下步骤：

    1 初始化权重和偏置（例如，随机初始化）。

    2 将训练数据输入神经网络中进行前馈，以生成输出。

    3 将输出与正确输出进行比较，以获取误差。

    4 基于误差计算权重和偏置的变化。

    5 将变化通过神经网络进行反向传播。

    对于给定的迭代次数或满足停止条件时，重复步骤2-5。

    在步骤3-5中，我们将利用随机梯度下降（SGD）来确定权重和偏置的更新：

// train trains a neural network using backpropagation.
func (nn *neuralNet) train(x, y *mat.Dense) error {

    // Initialize biases/weights.
    randSource := rand.NewSource(time.Now().UnixNano())
    randGen := rand.New(randSource)

    wHidden := mat.NewDense(nn.config.inputNeurons, nn.config.hiddenNeurons, nil)
    bHidden := mat.NewDense(1, nn.config.hiddenNeurons, nil)
    wOut := mat.NewDense(nn.config.hiddenNeurons, nn.config.outputNeurons, nil)
    bOut := mat.NewDense(1, nn.config.outputNeurons, nil)

    wHiddenRaw := wHidden.RawMatrix().Data
    bHiddenRaw := bHidden.RawMatrix().Data
    wOutRaw := wOut.RawMatrix().Data
    bOutRaw := bOut.RawMatrix().Data

    for _, param := range [][]float64{
        wHiddenRaw,
        bHiddenRaw,
        wOutRaw,
        bOutRaw,
    } {
        for i := range param {
            param[i] = randGen.Float64()
        }
    }

    // Define the output of the neural network.
    output := new(mat.Dense)

    // Use backpropagation to adjust the weights and biases.
    if err := nn.backpropagate(x, y, wHidden, bHidden, wOut, bOut, output); err != nil {
        return err
    }

    // Define our trained neural network.
    nn.wHidden = wHidden
    nn.bHidden = bHidden
    nn.wOut = wOut
    nn.bOut = bOut

    return nil
}

    接着实现具体的反向传播逻辑：

// backpropagate completes the backpropagation method.
func (nn *neuralNet) backpropagate(x, y, wHidden, bHidden, wOut, bOut, output *mat.Dense) error {

    // Loop over the number of epochs utilizing
    // backpropagation to train our model.
    for i := 0; i < nn.config.numEpochs; i++ {

        // Complete the feed forward process.
        hiddenLayerInput := new(mat.Dense)
        hiddenLayerInput.Mul(x, wHidden)
        addBHidden := func(_, col int, v float64) float64 { return v + bHidden.At(0, col) }
        hiddenLayerInput.Apply(addBHidden, hiddenLayerInput)

        hiddenLayerActivations := new(mat.Dense)
        applySigmoid := func(_, _ int, v float64) float64 { return sigmoid(v) }
        hiddenLayerActivations.Apply(applySigmoid, hiddenLayerInput)

        outputLayerInput := new(mat.Dense)
        outputLayerInput.Mul(hiddenLayerActivations, wOut)
        addBOut := func(_, col int, v float64) float64 { return v + bOut.At(0, col) }
        outputLayerInput.Apply(addBOut, outputLayerInput)
        output.Apply(applySigmoid, outputLayerInput)

        // Complete the backpropagation.
        networkError := new(mat.Dense)
        networkError.Sub(y, output)

        slopeOutputLayer := new(mat.Dense)
        applySigmoidPrime := func(_, _ int, v float64) float64 { return sigmoidPrime(v) }
        slopeOutputLayer.Apply(applySigmoidPrime, output)
        slopeHiddenLayer := new(mat.Dense)
        slopeHiddenLayer.Apply(applySigmoidPrime, hiddenLayerActivations)

        dOutput := new(mat.Dense)
        dOutput.MulElem(networkError, slopeOutputLayer)
        errorAtHiddenLayer := new(mat.Dense)
        errorAtHiddenLayer.Mul(dOutput, wOut.T())

        dHiddenLayer := new(mat.Dense)
        dHiddenLayer.MulElem(errorAtHiddenLayer, slopeHiddenLayer)

        // Adjust the parameters.
        wOutAdj := new(mat.Dense)
        wOutAdj.Mul(hiddenLayerActivations.T(), dOutput)
        wOutAdj.Scale(nn.config.learningRate, wOutAdj)
        wOut.Add(wOut, wOutAdj)

        bOutAdj, err := sumAlongAxis(0, dOutput)
        if err != nil {
            return err
        }
        bOutAdj.Scale(nn.config.learningRate, bOutAdj)
        bOut.Add(bOut, bOutAdj)

        wHiddenAdj := new(mat.Dense)
        wHiddenAdj.Mul(x.T(), dHiddenLayer)
        wHiddenAdj.Scale(nn.config.learningRate, wHiddenAdj)
        wHidden.Add(wHidden, wHiddenAdj)

        bHiddenAdj, err := sumAlongAxis(0, dHiddenLayer)
        if err != nil {
            return err
        }
        bHiddenAdj.Scale(nn.config.learningRate, bHiddenAdj)
        bHidden.Add(bHidden, bHiddenAdj)
    }

    return nil
}

    接着声明一个工具函数，它帮助我们沿一个矩阵维度求和，同时保持另一个维度不变：

// sumAlongAxis sums a matrix along a particular dimension, 
// preserving the other dimension.
func sumAlongAxis(axis int, m *mat.Dense) (*mat.Dense, error) {

        numRows, numCols := m.Dims()

        var output *mat.Dense

        switch axis {
        case 0:
                data := make([]float64, numCols)
                for i := 0; i < numCols; i++ {
                        col := mat.Col(nil, i, m)
                        data[i] = floats.Sum(col)
                }
                output = mat.NewDense(1, numCols, data)
        case 1:
                data := make([]float64, numRows)
                for i := 0; i < numRows; i++ {
                        row := mat.Row(nil, i, m)
                        data[i] = floats.Sum(row)
                }
                output = mat.NewDense(numRows, 1, data)
        default:
                return nil, errors.New("invalid axis, must be 0 or 1")
        }

        return output, nil
}

    实现前向传播进行预测

    在训练完我们的神经网络之后，我们希望使用它进行预测。为此，我们只需要将一些给定的鸢尾花特征值输入到网络中进行前向传播，用来生成输出。

    有点像反向传播逻辑，不同之处在于，这里我们将返回生成的输出：

// predict makes a prediction based on a trained
// neural network.
func (nn *neuralNet) predict(x *mat.Dense) (*mat.Dense, error) {

    // Check to make sure that our neuralNet value
    // represents a trained model.
    if nn.wHidden == nil || nn.wOut == nil {
        return nil, errors.New("the supplied weights are empty")
    }
    if nn.bHidden == nil || nn.bOut == nil {
        return nil, errors.New("the supplied biases are empty")
    }

    // Define the output of the neural network.
    output := new(mat.Dense)

    // Complete the feed forward process.
    hiddenLayerInput := new(mat.Dense)
    hiddenLayerInput.Mul(x, nn.wHidden)
    addBHidden := func(_, col int, v float64) float64 { return v + nn.bHidden.At(0, col) }
    hiddenLayerInput.Apply(addBHidden, hiddenLayerInput)

    hiddenLayerActivations := new(mat.Dense)
    applySigmoid := func(_, _ int, v float64) float64 { return sigmoid(v) }
    hiddenLayerActivations.Apply(applySigmoid, hiddenLayerInput)

    outputLayerInput := new(mat.Dense)
    outputLayerInput.Mul(hiddenLayerActivations, nn.wOut)
    addBOut := func(_, col int, v float64) float64 { return v + nn.bOut.At(0, col) }
    outputLayerInput.Apply(addBOut, outputLayerInput)
    output.Apply(applySigmoid, outputLayerInput)

    return output, nil
}

    准备特征和期望数据

    下面我们需要准备鸢尾花的特征和期望数据，可以在加州大学官网下载：https://archive.ics.uci.edu/ml/datasets/iris

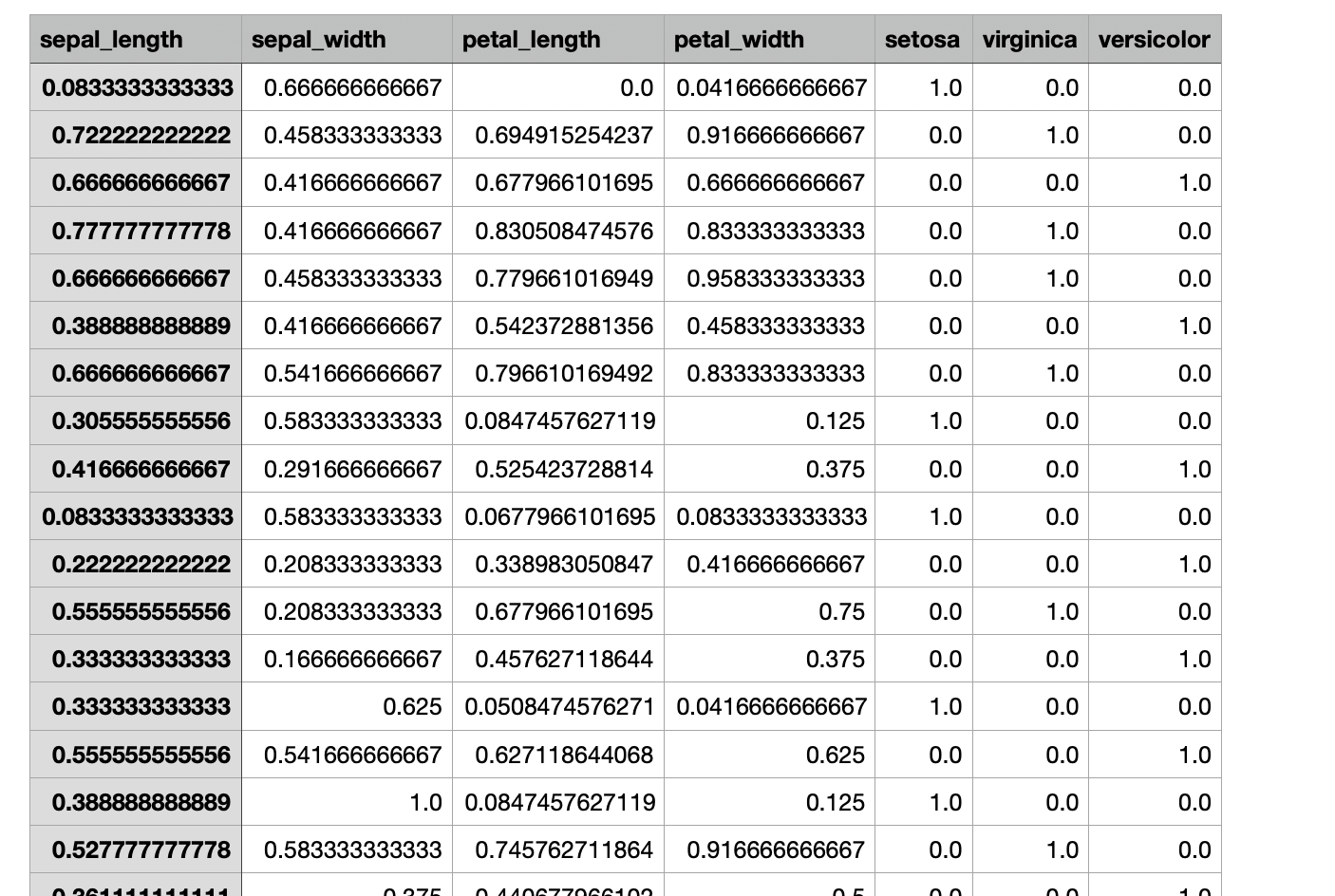
    这里包含花瓣和花蕊的具体数据，以及这些样本所对应的花的种类，分别对应上文提到的山鸢尾（Iris Setosa）、维吉尼亚鸢尾（Iris Virginica）和 变色鸢尾（Iris Versicolour），注意鸢尾花种类顺序分先后，分别对应上表中的数据。

    开始训练

    训练之前，需要安装基于Golang的浮点库：

go get gonum.org/v1/gonum/floats

    安装后之后，编写脚本：

package main

import (
	"encoding/csv"
	"errors"
	"fmt"
	"log"
	"math"
	"math/rand"
	"os"
	"strconv"
	"time"

	"gonum.org/v1/gonum/floats"
	"gonum.org/v1/gonum/mat"
)

// neuralNet contains all of the information
// that defines a trained neural network.
type neuralNet struct {
	config  neuralNetConfig
	wHidden *mat.Dense
	bHidden *mat.Dense
	wOut    *mat.Dense
	bOut    *mat.Dense
}

// neuralNetConfig defines our neural network
// architecture and learning parameters.
type neuralNetConfig struct {
	inputNeurons  int
	outputNeurons int
	hiddenNeurons int
	numEpochs     int
	learningRate  float64
}

func main() {

	// Form the training matrices.
	inputs, labels := makeInputsAndLabels("data/train.csv")

	// Define our network architecture and learning parameters.
	config := neuralNetConfig{
		inputNeurons:  4,
		outputNeurons: 3,
		hiddenNeurons: 3,
		numEpochs:     5000,
		learningRate:  0.3,
	}

	// Train the neural network.
	network := newNetwork(config)
	if err := network.train(inputs, labels); err != nil {
		log.Fatal(err)
	}

	// Form the testing matrices.
	testInputs, testLabels := makeInputsAndLabels("data/test.csv")

	// Make the predictions using the trained model.
	predictions, err := network.predict(testInputs)
	if err != nil {
		log.Fatal(err)
	}

	// Calculate the accuracy of our model.
	var truePosNeg int
	numPreds, _ := predictions.Dims()
	for i := 0; i < numPreds; i++ {

		// Get the label.
		labelRow := mat.Row(nil, i, testLabels)
		var prediction int
		for idx, label := range labelRow {
			if label == 1.0 {
				prediction = idx
				break
			}
		}

		// Accumulate the true positive/negative count.
		if predictions.At(i, prediction) == floats.Max(mat.Row(nil, i, predictions)) {
			truePosNeg++
		}
	}

	// Calculate the accuracy (subset accuracy).
	accuracy := float64(truePosNeg) / float64(numPreds)

	// Output the Accuracy value to standard out.
	fmt.Printf("\nAccuracy = %0.2f\n\n", accuracy)
}

// NewNetwork initializes a new neural network.
func newNetwork(config neuralNetConfig) *neuralNet {
	return &neuralNet{config: config}
}

// train trains a neural network using backpropagation.
func (nn *neuralNet) train(x, y *mat.Dense) error {

	// Initialize biases/weights.
	randSource := rand.NewSource(time.Now().UnixNano())
	randGen := rand.New(randSource)

	wHidden := mat.NewDense(nn.config.inputNeurons, nn.config.hiddenNeurons, nil)
	bHidden := mat.NewDense(1, nn.config.hiddenNeurons, nil)
	wOut := mat.NewDense(nn.config.hiddenNeurons, nn.config.outputNeurons, nil)
	bOut := mat.NewDense(1, nn.config.outputNeurons, nil)

	wHiddenRaw := wHidden.RawMatrix().Data
	bHiddenRaw := bHidden.RawMatrix().Data
	wOutRaw := wOut.RawMatrix().Data
	bOutRaw := bOut.RawMatrix().Data

	for _, param := range [][]float64{
		wHiddenRaw,
		bHiddenRaw,
		wOutRaw,
		bOutRaw,
	} {
		for i := range param {
			param[i] = randGen.Float64()
		}
	}

	// Define the output of the neural network.
	output := new(mat.Dense)

	// Use backpropagation to adjust the weights and biases.
	if err := nn.backpropagate(x, y, wHidden, bHidden, wOut, bOut, output); err != nil {
		return err
	}

	// Define our trained neural network.
	nn.wHidden = wHidden
	nn.bHidden = bHidden
	nn.wOut = wOut
	nn.bOut = bOut

	return nil
}

// backpropagate completes the backpropagation method.
func (nn *neuralNet) backpropagate(x, y, wHidden, bHidden, wOut, bOut, output *mat.Dense) error {

	// Loop over the number of epochs utilizing
	// backpropagation to train our model.
	for i := 0; i < nn.config.numEpochs; i++ {

		// Complete the feed forward process.
		hiddenLayerInput := new(mat.Dense)
		hiddenLayerInput.Mul(x, wHidden)
		addBHidden := func(_, col int, v float64) float64 { return v + bHidden.At(0, col) }
		hiddenLayerInput.Apply(addBHidden, hiddenLayerInput)

		hiddenLayerActivations := new(mat.Dense)
		applySigmoid := func(_, _ int, v float64) float64 { return sigmoid(v) }
		hiddenLayerActivations.Apply(applySigmoid, hiddenLayerInput)

		outputLayerInput := new(mat.Dense)
		outputLayerInput.Mul(hiddenLayerActivations, wOut)
		addBOut := func(_, col int, v float64) float64 { return v + bOut.At(0, col) }
		outputLayerInput.Apply(addBOut, outputLayerInput)
		output.Apply(applySigmoid, outputLayerInput)

		// Complete the backpropagation.
		networkError := new(mat.Dense)
		networkError.Sub(y, output)

		slopeOutputLayer := new(mat.Dense)
		applySigmoidPrime := func(_, _ int, v float64) float64 { return sigmoidPrime(v) }
		slopeOutputLayer.Apply(applySigmoidPrime, output)
		slopeHiddenLayer := new(mat.Dense)
		slopeHiddenLayer.Apply(applySigmoidPrime, hiddenLayerActivations)

		dOutput := new(mat.Dense)
		dOutput.MulElem(networkError, slopeOutputLayer)
		errorAtHiddenLayer := new(mat.Dense)
		errorAtHiddenLayer.Mul(dOutput, wOut.T())

		dHiddenLayer := new(mat.Dense)
		dHiddenLayer.MulElem(errorAtHiddenLayer, slopeHiddenLayer)

		// Adjust the parameters.
		wOutAdj := new(mat.Dense)
		wOutAdj.Mul(hiddenLayerActivations.T(), dOutput)
		wOutAdj.Scale(nn.config.learningRate, wOutAdj)
		wOut.Add(wOut, wOutAdj)

		bOutAdj, err := sumAlongAxis(0, dOutput)
		if err != nil {
			return err
		}
		bOutAdj.Scale(nn.config.learningRate, bOutAdj)
		bOut.Add(bOut, bOutAdj)

		wHiddenAdj := new(mat.Dense)
		wHiddenAdj.Mul(x.T(), dHiddenLayer)
		wHiddenAdj.Scale(nn.config.learningRate, wHiddenAdj)
		wHidden.Add(wHidden, wHiddenAdj)

		bHiddenAdj, err := sumAlongAxis(0, dHiddenLayer)
		if err != nil {
			return err
		}
		bHiddenAdj.Scale(nn.config.learningRate, bHiddenAdj)
		bHidden.Add(bHidden, bHiddenAdj)
	}

	return nil
}

// predict makes a prediction based on a trained
// neural network.
func (nn *neuralNet) predict(x *mat.Dense) (*mat.Dense, error) {

	// Check to make sure that our neuralNet value
	// represents a trained model.
	if nn.wHidden == nil || nn.wOut == nil {
		return nil, errors.New("the supplied weights are empty")
	}
	if nn.bHidden == nil || nn.bOut == nil {
		return nil, errors.New("the supplied biases are empty")
	}

	// Define the output of the neural network.
	output := new(mat.Dense)

	// Complete the feed forward process.
	hiddenLayerInput := new(mat.Dense)
	hiddenLayerInput.Mul(x, nn.wHidden)
	addBHidden := func(_, col int, v float64) float64 { return v + nn.bHidden.At(0, col) }
	hiddenLayerInput.Apply(addBHidden, hiddenLayerInput)

	hiddenLayerActivations := new(mat.Dense)
	applySigmoid := func(_, _ int, v float64) float64 { return sigmoid(v) }
	hiddenLayerActivations.Apply(applySigmoid, hiddenLayerInput)

	outputLayerInput := new(mat.Dense)
	outputLayerInput.Mul(hiddenLayerActivations, nn.wOut)
	addBOut := func(_, col int, v float64) float64 { return v + nn.bOut.At(0, col) }
	outputLayerInput.Apply(addBOut, outputLayerInput)
	output.Apply(applySigmoid, outputLayerInput)

	return output, nil
}

// sigmoid implements the sigmoid function
// for use in activation functions.
func sigmoid(x float64) float64 {
	return 1.0 / (1.0 + math.Exp(-x))
}

// sigmoidPrime implements the derivative
// of the sigmoid function for backpropagation.
func sigmoidPrime(x float64) float64 {
	return sigmoid(x) * (1.0 - sigmoid(x))
}

// sumAlongAxis sums a matrix along a
// particular dimension, preserving the
// other dimension.
func sumAlongAxis(axis int, m *mat.Dense) (*mat.Dense, error) {

	numRows, numCols := m.Dims()

	var output *mat.Dense

	switch axis {
	case 0:
		data := make([]float64, numCols)
		for i := 0; i < numCols; i++ {
			col := mat.Col(nil, i, m)
			data[i] = floats.Sum(col)
		}
		output = mat.NewDense(1, numCols, data)
	case 1:
		data := make([]float64, numRows)
		for i := 0; i < numRows; i++ {
			row := mat.Row(nil, i, m)
			data[i] = floats.Sum(row)
		}
		output = mat.NewDense(numRows, 1, data)
	default:
		return nil, errors.New("invalid axis, must be 0 or 1")
	}

	return output, nil
}

func makeInputsAndLabels(fileName string) (*mat.Dense, *mat.Dense) {
	// Open the dataset file.
	f, err := os.Open(fileName)
	if err != nil {
		log.Fatal(err)
	}
	defer f.Close()

	// Create a new CSV reader reading from the opened file.
	reader := csv.NewReader(f)
	reader.FieldsPerRecord = 7

	// Read in all of the CSV records
	rawCSVData, err := reader.ReadAll()
	if err != nil {
		log.Fatal(err)
	}

	// inputsData and labelsData will hold all the
	// float values that will eventually be
	// used to form matrices.
	inputsData := make([]float64, 4*len(rawCSVData))
	labelsData := make([]float64, 3*len(rawCSVData))

	// Will track the current index of matrix values.
	var inputsIndex int
	var labelsIndex int

	// Sequentially move the rows into a slice of floats.
	for idx, record := range rawCSVData {

		// Skip the header row.
		if idx == 0 {
			continue
		}

		// Loop over the float columns.
		for i, val := range record {

			// Convert the value to a float.
			parsedVal, err := strconv.ParseFloat(val, 64)
			if err != nil {
				log.Fatal(err)
			}

			// Add to the labelsData if relevant.
			if i == 4 || i == 5 || i == 6 {
				labelsData[labelsIndex] = parsedVal
				labelsIndex++
				continue
			}

			// Add the float value to the slice of floats.
			inputsData[inputsIndex] = parsedVal
			inputsIndex++
		}
	}
	inputs := mat.NewDense(len(rawCSVData), 4, inputsData)
	labels := mat.NewDense(len(rawCSVData), 3, labelsData)
	return inputs, labels
}

    代码最后将测试集数据导入，并且开始进行预测：

// Form the testing matrices.
	testInputs, testLabels := makeInputsAndLabels("data/test.csv")

	fmt.Println(testLabels)

	// Make the predictions using the trained model.
	predictions, err := network.predict(testInputs)
	if err != nil {
		log.Fatal(err)
	}

	// Calculate the accuracy of our model.
	var truePosNeg int
	numPreds, _ := predictions.Dims()
	for i := 0; i < numPreds; i++ {

		// Get the label.
		labelRow := mat.Row(nil, i, testLabels)
		var prediction int
		for idx, label := range labelRow {
			if label == 1.0 {
				prediction = idx
				break
			}
		}

		// Accumulate the true positive/negative count.
		if predictions.At(i, prediction) == floats.Max(mat.Row(nil, i, predictions)) {
			truePosNeg++
		}
	}

	// Calculate the accuracy (subset accuracy).
	accuracy := float64(truePosNeg) / float64(numPreds)

	// Output the Accuracy value to standard out.
	fmt.Printf("\nAccuracy = %0.2f\n\n", accuracy)

    程序输出：

&{{31 3 [0 1 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 1 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 1 0 0 1 0 0 0 1 0 1 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 0 0 0 1 0 0 1 0 0 0] 3} 31 3}

Accuracy = 0.97

    可以看到，一共31个测试样本，只错了3次，成功率达到了97%。

    当然，就算是自己实现的小型神经网络，预测结果正确率也不可能达到100%，因为机器学习也是基于概率学范畴的学科。

    为什么使用Golang？

    事实上，大部分人都存在这样一个刻板影响：机器学习必须要用Python来实现。就像前文所提到的，机器学习和Python语言并不存在因果关系，我们使用Golang同样可以实现神经网络，同样可以完成机器学习的流程，编程语言，仅仅是实现的工具而已。

    但不能否认的是，Python当前在人工智能领域的很多细分方向都有比较广泛的应用，比如自然语言处理、计算机视觉和机器学习等领域，但是并不意味着人工智能研发一定离不开Python语言，实际上很多其他编程语言也完全可以替代Python，比如Java、C++、Golang等等。

    机器学习相关业务之所以大量使用Python，是因为Python有着极其丰富的三方库进行支持，能够让研发人员把更多的精力放在算法设计和算法训练等方面，说白了，就是不用重复造轮子，提高研发团队整体产出的效率，比如面对基于Python的Pytorch和Tensorflow这两个颠扑不破的深度学习巨石重镇，Golang就得败下阵来，没有任何优势可言。

    所以，单以人工智能生态圈的繁荣程度而论，Golang还及不上Python。

    结语

    至此，我们就使用Golang完成了一个小型神经网络的实现，并且解决了一个真实存在的分类问题。那么，走完了整个流程，我们应该对基于神经网络架构的机器学习过程有了一个大概的了解，那就是机器学习只能解决可以被解决的问题，有经验或者相关知识储备的人类通过肉眼也能识别鸢尾花的种类，机器学习只是帮我们提高了识别效率而已，所以，如果还有人在你面前吹嘘他能够用机器学习来预测A股价格赚大钱，那么，他可能对机器学习存在误解，或者可能对A股市场存在误解，或者就是个纯骗子，三者必居其一。